
よく±2SDって見るけどなんですか?

標準偏差のことですね
ばらつきを知る上で重要です
学校の試験が返ってきたときに気になることはなんですか?
もちろん点数は気になると思いますが
もう一つ気になることはありませんか?
そうですね
周りの人と比較して自分がどの程度できたのかということですよね
80点の答案が返ってきて嬉しくて友達に自慢したところ
周りの友達はみんな90点以上でした・・・(親にはみんなの点数はだまっておこう)
ちなみに偏差値もこの標準偏差を用いて計算された数字です
この周りと比較するときにばらつき・分布を知る必要があります
ばらつきを示すものとして
「標準偏差:standard deviation,SD」
「範囲:range」
「四分位範囲:inter-quartile range」
があります

3つもあるんですか?もう自分には無理なので諦めま・・・

諦めたらそこで試合終了ですよ?
大丈夫です
サルでもわかるように簡単に説明します
この記事を読んで出来るようになること
・標準偏差の使い方がわかる
・標準偏差が使えない状況がわかる
・標準偏差が使えない状況にも対応できる
標準偏差:SD
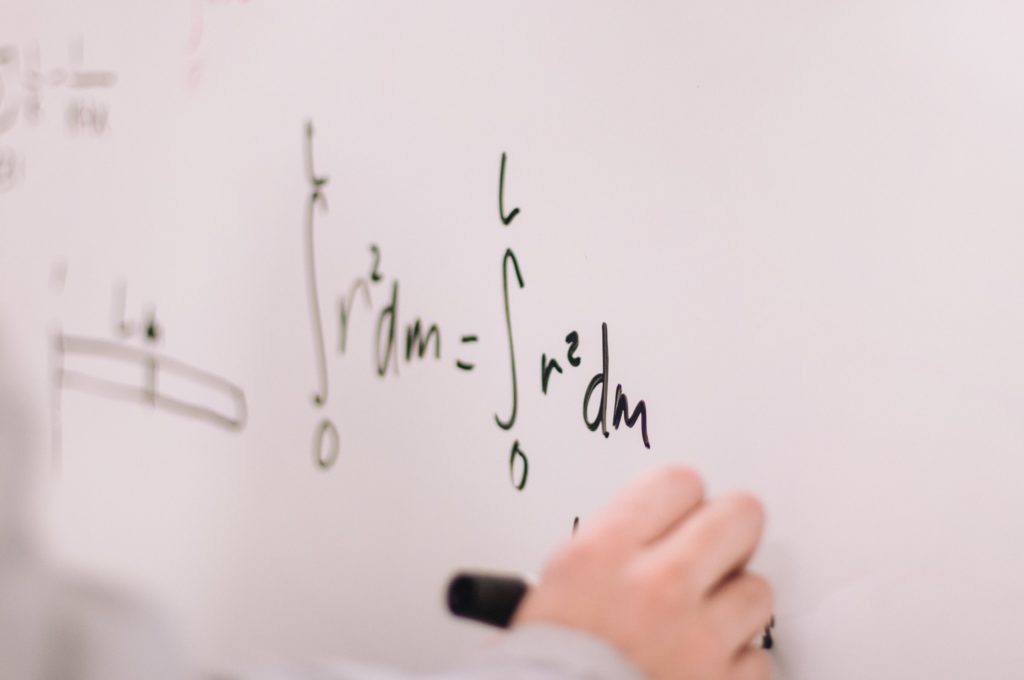
標準偏差は平均値の後に書かれています
また次のように書かれていることもあります
それでは具体的な例を用いて考えてみましょう
あなたが今30人のクラスにいるとしましょう
身体測定を行いました結果は以下のようになりました
ここでポイントのおさらいをしましょう
標準偏差の使い道
平均値ー標準偏差×2〜平均値+標準偏差×2の間に存在する
どうですか?
思っていたよりも単純ではありませんか?
もちろん標準偏差を求める式だの考えると話は難しくなりますが
まずは標準偏差というものが何を意味するのか
YouTube:動画を見ることができるサイト
使い方:暇つぶしや勉強に使える
これで十分です
YouTubeに動画をUpする方法を知らなくても困りませんよね?
つまり先程の例に戻ると標準偏差を使うことで
クラスの学生の95%は
170.3ー2×4.5から170.3+2×4.5cm
161.3〜179.3cmの間の身長であることがわかります
それでは試しに次のクラスの身長の分布を考えてみてください
クラスB 平均 170cm 標準偏差 5cm
クラスC 平均 170cm 標準偏差10cm
計算できましたか?
クラスAの95%は165〜175cmの間の身長である(分布の幅10cm)
クラスBの95%は160〜180cmの間の身長である(分布の幅20cm)
クラスCの95%は150〜190cmの間の身長である(分布の幅40cm)
この3つのクラスを比較して気がつくことがありませんか?
そうです
さらに標準偏差には他の使い道があります
女子 平均 158cm 標準偏差 2cm
男子の95%は164〜176cm
女子の95%は154〜162cm
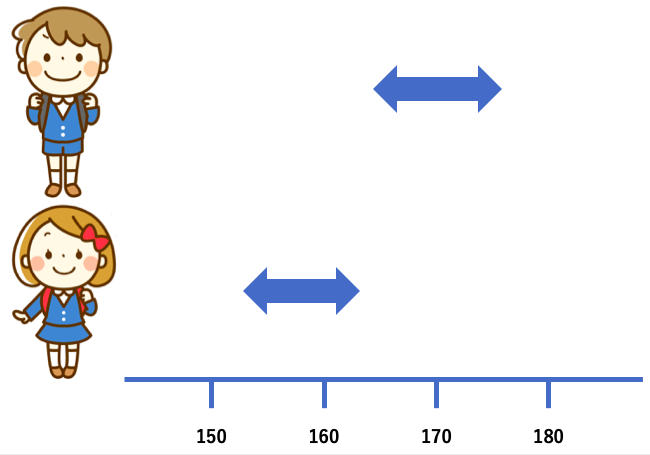
女子よりも男子の方が身長が高いことが予想できます
一方で
女子 平均 158cm 標準偏差 3cm
この場合
男子の95%は160〜180cm
女子の95%は152〜164cm

女子よりも男子の方が身長が高そうですが
重なる部分もあるのでハッキリとは言えないですね
グループ間に差があるかどうかをある程度推測することができます
標準偏差が使えない状況
平均値があるということは中央値の場合は使えるのか?という疑問が出て来ますね
「平均値と中央値って同じことじゃないの?」と思ったヒトはこちらをご覧ください

平均値はデータに偏りがない時
中央値はデータに偏りがある時に使いましたね?
つまりデータに偏りがある
平均値が使えない状況では
先程までの便利な標準偏差は全く役に立ちません(これまでの時間返せ!!)
実際に考えてみましょう
クラス10人のお年玉を考えてみましょう
5,000円が2人
7,000円が3人
10,000円が4人
100,000円が1人(IT企業の社長の息子)
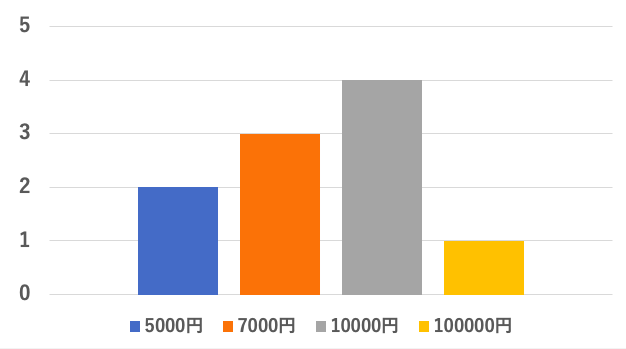
データに偏りがありますね
計算すると
平均値は17,100円 標準偏差は27,700円となります
お年玉でもらっている金額の95%は-38,300円〜72,500円の間になります
・・・
もはや意味がわかりませんね
このようにデータに偏りがあると使えないんです
安心してください!そんな時の対応も教えますよ!
四分位範囲
これは得られたデータの小さい方25%と大きい方25%のデータを捨て
残った中央50%のデータ範囲を求めたものです
ピンと来ませんよね?
先程のお年玉の例をみていきましょう
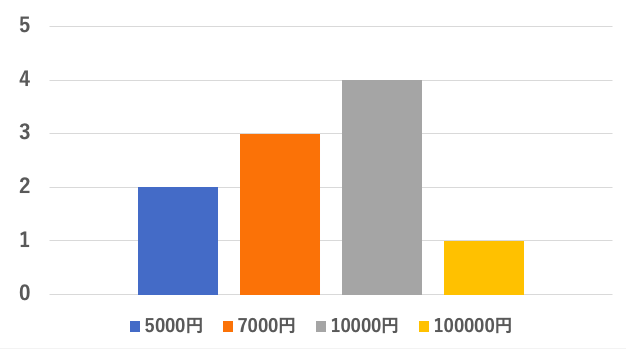
計算すると
中央値は8,500円
小さい方25%は7,000円
大きい方75%は10,000円です
ここで一番簡単な「範囲」もついでに説明します
「範囲」は最小〜最大を示したものです
お年玉 中央値8,500円(範囲5,000円〜100,000円)
これを見るとこのクラスでは
一番少ないヒトは5,000円
一番多いヒトは100,000円
8,500円程度もらっているヒトが多いんだなとわかります
さらに四分位範囲を用いると
お年玉 中央値8,500円(四分位範囲7,000円〜10,000円)(範囲5,000円〜100,000円)
クラスの半分のヒトは7,000〜10,000円もらっていることがわかります
データに偏りがある場合 中央値と四分位範囲でバラつきがわかる
参考文献







コメント